Article of the Month - August 2023
|
Affordable GNSS PPP Results as Constraints for
Pressure Time Series Offshore
Johnson Oguntuase, Uchenna Nwankwo, Stephan Howden,
USA
This article in .pdf-format
(16 pages)
This paper has been successfully peer reviewed and presented at the
FIG Working Week 2023 in Orlando, Florida. The authors describe
a new water level measurement technique for tidal datum
extension at offshore locations in addressing vandalization
challenges with GNSS buoys utilizing short-term PPP results from an
affordable GNSS receiver aboard a USV and a pressure sensor deployed
on the seafloor.
The paper was at the conference awarded with the NavXperience Price.

SUMMARY
This paper discusses offshore water level measurements and the
accuracies possible using affordable GNSS receivers (<$2000). The goal
is to develop an affordable and straightforward technique capable of
continuous and accurate water level measurements at remote locations
towards addressing the uncertainties inherent in the tidal datum
transformation model offered by NOAA’s Vdatum. This technique can be
used either directly for tidal datum transfer when 30 plus days of GNSS
data acquisition is possible or in short-term simultaneous observations
with a seafloor-mounted pressure gauge to reference the longer term (30+
days) pressure time series to the ellipsoid before tidal datum transfer
is performed. We applied precise point positioning (PPP) results from an
affordable GNSS receiver to constrain pressure sensor measurements to
the ellipsoid. Limiting Vdatum uncertainties below 10 cm at a 95 %
confidence level would require that GNSS height uncertainties be less
than 5 cm in the error budget. It is then desirable to investigate the
order of PPP vertical positioning accuracies possible with such a
receiver on a dynamic platform at sea. We conducted two experiments at
different locations offshore using GNSS+INS sensors to validate the
affordable PPP vertical positioning results. The GNSS+INS sensors in the
post-processed kinematic (PPK) strategy validate the affordable PPP
vertical position results. We note that the second experiment’s results
are more consistent than the first following accurate lever-arms
measurements for the GNSS antennas installed on an Echo boat (small
uncrewed surface vehicle). Comparing water level moving averages between
the two processing strategies shows a mean difference of 4 cm. That
result compares instantaneous GNSS heights from the affordable receiver
without accounting for induced heave, suggesting that attitude
measurements at sea for short lever arms are negligible. Briefly
discussed is the preliminary validation of the tidal datum determination
offshore using the affordable vertical positions as the constraint.
1. INTRODUCTION
This study aims to show the utility of affordable GNSS receivers on a
floating platform, such as a buoy or Autonomous Surface Vessel, in a
newly developed approach to vertically reference seafloor pressure
measurements of water level to a geodetic reference system. This would
allow a seafloor pressure record to be used in a tidal datum transfer
exercise to obtain tidal datums to the ellipsoid and used to validate
and improve tools such as NOAA’s VDatum (Parker et al., 2003) that, for
example, allow hydrographic surveys to be referenced relative to the
ellipsoid, eliminating complications of heave and tidal measurements,
and then converted to chart datum (Mean Lower Low Water in the U.S.).
The GNSS market has seen rapid developments in GNSS hardware and
allied sensors required for autonomous driving technology implementation
driven by investments in the autonomous car industry. Hence the
proliferation of different GNSS hardware grades ranging from smartphone
chipsets to low-cost/mass markets development kits capable of tracking
single- or multi-constellations and single- or multi-frequencies. The
rapid proliferation of GNSS hardware enables various location-based
applications, consequently driving studies on affordable/mass-market
GNSS hardware. Many studies (Aggrey et al., 2019; Banville et al., 2019;
Gill et al., 2018; Nie et al., 2020; Oguntuase, 2020) exist on GNSS
hardware characteristics and performances in different positioning and
navigation strategies. The mass market literature describes some
non-geodetic GNSS receivers (capable of combining single- or
multi-frequency and single- or multi-GNSS) as low-cost, mass-market,
cost-effective, or affordable. That classification stems from their
tracking quality, prices (tens of dollars to a few hundred), and overall
product features.
Some FIG publications address related studies (Arnell et al., n.d.;
Lipatnikov & Shevchuk, 2019; Weston & Dr. Volker Schwieger, 2010).
However, studies on low-cost/affordable GNSS receivers for precise point
positioning (PPP) at offshore locations are scarce. In this work, we
demonstrate the potential of an affordable GNSS receiver (<$2000) in
addressing the uncertainties inherent in the tidal datum extension
offshore. For instance, Nwankwo et al., 2020 discuss errors in NOAA’s
Vdatum model (Parker et al., 2003) for seamless transformations between
different height systems in the United States.
The first reduction tidal datums are average levels, ranges, or tide
phases, computed over the lunar nodal cycle (~19 years). Many water
level gauges have not been in operation for 19 years, and so methods
have been developed to use simultaneous measurements from a short-term
(subordinate) gauge and a long-term control (primary) gauge, and the
19-year datums from the control gauge, to estimate equivalent 19-year
datums for the subordinate gauge (Gill and Schultz, 2001). Swanson
(1974) estimated the uncertainties in tidal datums from tidal datum
transfers for varying lengths of simultaneous subordinate and primary
water level records and obtained values of 0.040 m for a 1-month
simultaneous record on the east and west coasts and 0.055 m on the coast
of the Gulf of Mexico. In the context of the allowed Total Vertical
Uncertainty allowed for an Order 1a hydrographic survey in 20 m of water
of 0.564 m or Special Order of 0.292 m (IHO, 2020), these uncertainties
are 7% and 14% for Order 1a and Special Order, respectively on the west
and east coasts and 14% and 19%, respectively on the Gulf Coast.
Information on geodetically referenced offshore tidal datums can be
obtained using GNSS buoys (e.g., Hocker and Wardell, 2010; Nwankwo et
al., 2020). However, on the coastal water of the northern Gulf of
Mexico, the authors have not been successful in keeping a moored GNSS
buoy out for more than a couple of weeks without it being vandalized, as
reported in Nwankwo et al., 2020. Utilizing the hydrostatic equation,
information on the density of the water column, and sea level barometric
pressure, a seafloor-mounted pressure gauge can measure the water levels
above it, but there is no absolute reference for the measurements.
However, a short-term (>= 6 hours) simultaneous geodetically measured
sea level from a buoy or ASV and a pressure gauge can be used to
reference, geodetically, the water levels from the pressure gauge. The
resulting water level can then be used in a tidal datum transfer.
In this work, we describe the concept where a 30-day GNSS observation
is unavailable but uses 6-hour PPP results (or more) as constraints for
pressure measurements (> 30 days). Next, we evaluate the PPP results
using the affordable GNSS receiver aboard an uncrewed surface vehicle
(USV) at an offshore location relative to post-processed kinematic (PPK)
results from co-located GNSS+INS hardware. Though GNSS buoy for tidal
datum determination is not new (André et al., 2013; Bisnath et al.,
2003; Cheng et al., 2004; Dodd, 2009; Hocker & Wardwell, 2010; Knight et
al., 2020; Lin et al., 2017), evaluating the PPP results from the
affordable GNSS receiver becomes essential as we note that such studies
are scarce. This paper presents the preliminary results of 30-day water
level observations using the PPP results as constraints for pressure
measurement. However, we limit our discussions to concept descriptions
and PPP accuracies at offshore locations. Since it is logical to
separate oceanographic computations from GNSS computations, we will
discuss the seafloor data, the analysis, and tidal datum transfer in a
follow-up paper.
2. EXPERIMENT DESIGN
Figure 1 presents the overview of the experiment
design, providing a roadmap to reproducing our results. The procedure is
as follows:
- Collect co-located GNSS and pressure measurements at an offshore
location
- Validate PPP-derived water level from an affordable GNSS
receiver, using results from a geodetic grade GNSS+INS sensor in the
PPK strategy
- Validate seafloor pressure data.
- Constrain the seafloor data to a reference ellipsoid (e.g.,
WGS84 or NAD83 ellipsoid)
- Prepare preliminary water levels from the seafloor data
- Compute and validate tidal datums and water levels
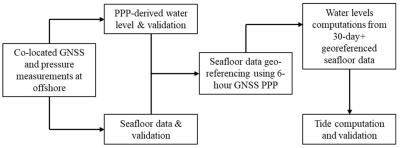
Figure 1 Experiment design flowchart.
As we mentioned in the introduction, details about seafloor data
validation and datum computations will come in a follow-up paper. We
demonstrate the repeatability of our results using the GNSS PPP and
pressure measurement approach for determining water levels by acquiring
data in two experimental setups that utilized an affordable GNSS
receiver, RBR Concerto CTD, RBR Digiquartz pressure sensor, and a
Teledyne/RDI ADCP (all oceanographic sensors housed in one single
underwater package), in separate deployments. Table 1
lists the sensors and the manufacturer’s name. It bears repeating that
the GNSS+INS sensor is only required to verify the affordable GNSS PPP
results offshore.

2.1 Experiment Locations
The first experiment occurred on May 27, 2021, at 29.9858N, 088.5379W
(Figure 2). We deployed a USV (EchoBoat) housing a Septentrio Mosaic
GNSS receiver and a survey-grade GNSS+INS from one of the University of
Southern Mississippi’s (USM) research vehicles, R/V Point Sur. The
second experiment occurred at 26.61589N, 88.41786W on March 1, 2022,
using the same GNSS receiver and tactical-grade GNSS+INS hardware aboard
a different USV (SeaTrac).
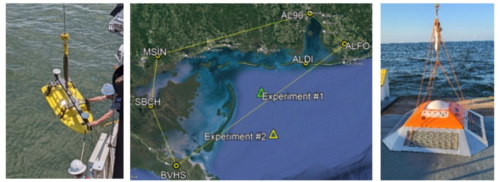
Figure 2 Left panel: EchoBoat deployment. Center
panel: experiment #1 and #2 locations: 52.4 and 78.6 km from the nearest
CORS (ALDI). PCLA, DSTN, and PNMA (are towards the east but not shown);
they enclosed location #2 in the CORS network. Right panel: Bottom
package deployment.
2.2 Operational Concept
GNSS-derived water level measurement technique is well-known (André
et al., 2013; Bisnath et al., 2003; Cheng et al., 2004; Dodd, 2009;
Hocker & Wardwell, 2010; Knight et al., 2020; Lin et al., 2017) and has
been proposed for water level observations, tidal datum extensions, and
datum improvements (Bisnath et al., 2003; Cheng et al., 2004; Dodd,
2009; Hocker & Wardwell, 2010). However, utilizing the technique for
tidal datum extension offshore would require at least 30-day GNSS water
level observations to estimate the tidal signal constituents.
Furthermore, such observation aboard a buoy or a USV may utilize quality
and cost-effective sensors like the affordable GNSS receiver.
The new concept requires sea surface deployment of a GNSS buoy or a
USV with GNSS onboard and a seafloor deployment of a pressure sensor.
The GNSS buoy, or USV with GNSS, need only be moored or kept on the
station long enough to compute the separation (H + O + D) value to the
desired accuracy, where H, O, and D are the ellipsoidal height, O is the
GNSS antenna offset above the sea surface, and D is the water depth from
the sea surface. It can then be removed to avoid vandalization, and the
bottom mooring can collect offshore water level records for 30 days or
more for tidal datum determination. One advantage of using the USV’s
station-keeping command is the ease of maintaining the exact location as
the deployed bottom package in autopilot mode. That feature allows the
vessel intermittently return to the preset location once it drifts out
of the redefined radius. In addition, the bottom package is equipped
with mooring flotation devices, which allows using acoustic releases for
retrieval. That concepts also preclude the bottom package vandalization.
Figure 3 describes the operational concept where the water depth D is
computed from the hydrostatic equation using the bottom, surface
temperature, and salinity values for density computation. The offset
from the USV to the water line is measured as O, and PPP processing is
used to measure the GNSS antenna height from WGS84 and transformed to
NAD83 ellipsoid.
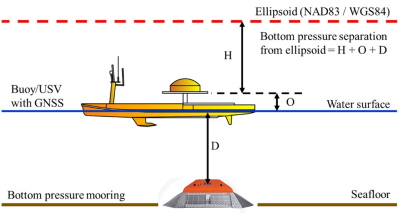
Figure 3 The operational concept uses a GNSS receiver installed on
either a buoy or a USV and a bottom package containing a pressure sensor
to estimate seafloor separation from the ellipsoid.
3. PROCESSING STRATEGY
Since numerous publications exist on GNSS processing strategies and
algorithms, we omit that discussion here due to page limit restrictions.
Hence the focus on concepts and the results. We used JPL’s GipsyX and
Hexagon-Novetel GrafNav PPP processing engines for the PPP data
processing for the data acquired with the affordable GNSS receiver. For
the GNSS+INS dataset, we used the Applanix POSPAC MMS’s Smartbase
processing engine. The PPP processing accounted for Earth deformations
(ocean loading, Earth tide, and pole tides). However, validating the
offshore PPP results is not straightforward, as the reference solutions,
in other words, the survey-grade GNSS+INS navigation solutions required
for the comparison, posed some challenges.
Such a challenge is typical whenever remote locations are outside the
CORS network, precluding accurate correction estimates for the virtual
reference station in the virtual reference station (VRS) or network PPK
strategy. Since ionospheric-free combinations efficiently mitigate that
error, the major challenge is the wet and dry tropospheric delays, which
deteriorate as distances increase from reference stations. In addressing
that challenge, we ensured the GNSS+INS dataset enclosure within the
CORS network for high-quality PPK results needed to validate the PPP.
All the GNSS processing used the products from the Center for Orbit
Determination in Europe (CODE).
All processing accounted for lever arms measurements, GNSS antenna
phase center, and offsets corrections to reduce GNSS ellipsoidal heights
to the sea surface. The first experiment used measuring tape to
determine the offsets, while the second used the total station
technique. Though it should be intuitive why precise lever arm
determination is essential, the results in the second experiment and the
subsequent summary emphasize that regardless of whether the vessels
involved are small or large. Additionally, following previous
discussions on tilt measurements to water level (Dodd, 2009; Hocker &
Wardwell, 2010; Lin et al., 2017), we investigate whether tilt
measurements in accounting for induced heave play a significant role
when the antenna lever arm less than a meter, as in both experiments.
RESULTS
One of the goals of this work is to justify using affordable GNSS
receivers with reasonable quality for high-accuracy kinematic PPP in
GNSS water level determination. Hence, we briefly examine the phase
residuals in different ionospheric-free combinations for different
constellations; we describe the PPP results (from affordable GNSS
receiver) and their validation relative to the PPK results (from
survey-grade GNSS+INS); we present the validation summary statistics and
the presents the pressure measurement results.
4.1 GNSS Data Quality Issues
Figure 4 (left panel) shows the number of satellites
(SVs) used in GipsyX PPP solutions for data acquired at Experiment
location #1, and Figure 4 (right panel) shows the phase residuals. Over
the seven-hour observation period, the number of GPS (G) SVs used for
the PPP solution is consistently higher than others. GPS contribution to
the multi-GNSS PPP solution ranges between seven and twelve SVs, while
BeiDou (C) and GLONASS (R) contributions are between four and nine. The
effects of those contributions appear in the phase residuals in the
panel to the right, revealing GPS with the best phase residuals – the
95% statistic is 2.6 cm. The histograms show narrow distributions for
GPS, GLONASS, and Galileo, whereas BeiDou’s distribution is wide.
Consequently, the GPS, GLONASS, and Galileo’s contribution to PPP
solutions offshore should yield more reliable results without the BeiDou
system when using CODE products.
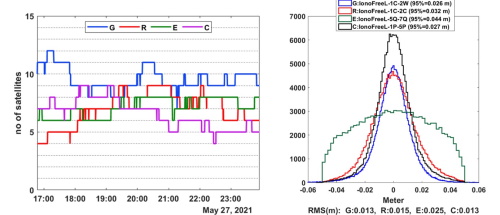
Figure 4: Left panel: number of satellites included
in GipsyX PPP solution at Experiment location #1. Right panel: carrier
phase residual distribution and the corresponding RMS values.
4.2 PPP Results
Figure 5 and Figure 6 (left panels)
present the PPP-derived water level time series (1 Hz) for 7- and 8-hour
observations from the affordable GNSS receiver. The right panels in
those figures show the PPK-derived water level time series (50 Hz) from
the GNSS+INS hardware. A 3-minute low-pass filter (LPF) cutoff (3-minute
moving average) is applied to all datasets to remove high-frequency
signals such as the surface gravity waves. The blue and red lines in the
figures represent the filtered water levels from the PPP (GNSS-only) and
PPK (GNSS+INS) results, respectively.
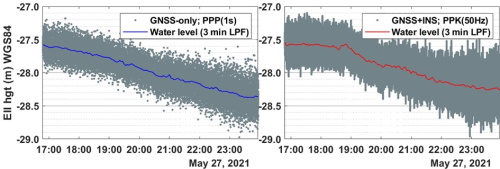
Figure 5 Instantaneous water levels (gray dots) at
experiment location #1. Left panel: PPP results (1 Hz) from affordable
GNSS. Right panel: PPK results from survey-grade GNSS+INS (50 Hz).
The blue and red lines are the water levels using the 3-minute LPF
cutoff.
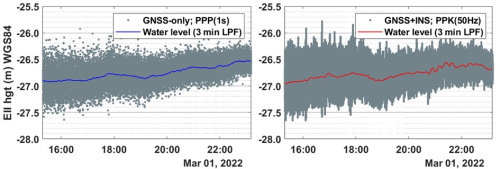
Figure 6 Instantaneous water levels (gray dots) at experiment
location #2. The graphics description is the same as described in Figure
5.
4.3 Kinematic PPP Validation
Figure 7 and Figure 8 summarize the
averaged water level results. The serial difference in water levels
derived from the two hardware and processing strategies offers an
insight into the PPP quality obtainable with a mass market GNSS receiver
on a dynamic offshore platform. The histograms in the left panels of
those figures describe the PPP versus PPK differences. Table 2
summarises the statistics. The 95% ordered statistic for the water level
differences at location #1 and location #2 are 14 and 11 cm,
respectively. The means are 7.9 and 0.5 cm, while the standard
deviations (1 sigma) are 3.9 and 5.4 cm, respectively. The difference
histogram at location #1 (Figure 7) shows a bias
between the PPP and PPK solutions. We attribute that to the lever arm
measurement quality. In contrast with the histogram at location 2 (Figure
8), the bias is near zero (5 mm). Again that emphasizes the
need for precise lever arm measurements with a total station or any
other precise measurement method irrespective of the vessel size.
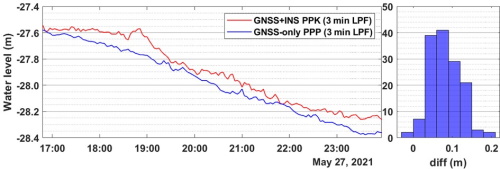
Figure 7 Left panel: averaged water levels from
GNSS-only and GNSS PPK results aboard EchoBoat (USV) location #2. Right
panel: averaged water level difference.
Designating the PPK results as the reference solution, assuming it
has better positioning quality than the PPP results, the statistics
suggest the worst PPP positioning quality is 14 cm relative to the PPK.
Though typical uncertainties for PPK-derived vertical position is about
5 cm, vertical uncertainties for kinematic PPP are slightly higher.
Notably, a 10-cm difference in kinematic PPP vertical positions is not
entirely outside typical kinematic PPP results using the traditional PPP
algorithm, which does not explicitly account for instrument code- and
phase biases, resulting in a non-integer ambiguity resolution. However,
an improvement in that vertical positioning accuracy with the receiver
is possible by eliminating data with non-gaussian distributing from
contribution to the PPP solution.
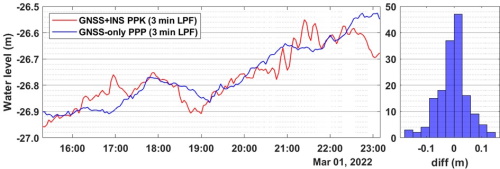
Figure 8 Left panel: averaged water levels from GNSS-only and GNSS
PPK results aboard SeaTrac (USV) at location #2. Right panel: averaged
water level difference.
Intuitively, one may suspect the induced-heave effect on the
PPP-derived water level averages since the PPP processing does not
account for the roll and pitch effects in the GNSS-only observations.
However, we quantified that effect by applying the roll and pitch
results from the GNSS+INS hardware to the affordable GNSS receiver’s
lever arm using Equation 1.
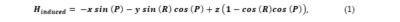
Vector [x, y, z] is the antenna lever arms from the vessel’s /
platform’s reference origin, with x pointing towards the bow in a
right-handed system, y pointing to the port, and z pointing in the up
direction, P and R are the roll and pitch angles (Hare et al., 1995).
The antenna lever arms on both vessels in the two experiments, ordered
as [x, y, z], are [1.371,0.015,0.343]_m and [-0.396,0.007,0.4650]_m. The
roll and pitch enviroments for the experiment locations are listed in
Table 2. Those values indicate the vessel’s attitude at sea, which
explains why the PPP results match the reference solutions (GNSS+INS) in
the experiment at location #1 compared to the results in location #2.
Another reason for the better roll-pitch environment at location two is
that the platform (SeaTrac) is larger than the Echo-Boat. Also, SeaTrac
operated in autopilot mode, unlike the Echo-Boat, which lost its
navigation and autopilot functionality at sea, thus requiring mooring at
the observation station.

Passing the instantaneous PPP results for experiment 1 with the
induced-heave corrections applied through the 3-minute LPF shows that
the resulting water levels have a near-zero difference (1 cm) for most
epochs (75th percentile) compared to the statistics for water levels
from GNSS-only PPP results without induced-heave corrections. However,
LPF reduces the induced heave from ± 13 cm in extreme cases (outside
0.01 and 99.99 percentile bounds) to near zero (± 0.3 cm). That agrees
somewhat with Dodd, 2009’s comment about the induced heave effect
reducing drastically to ~ 2 cm from 10 cm in a 6-minute LPF
cutoff. The induced heave effects and characteristics in experiment 2
results are similar to those described afore
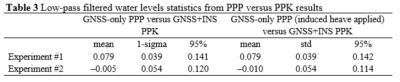
Table 3 summarizes the statistics comparing PPP results with and
without induced heave applied relative to the GNSS+INS solutions.
Comparing the 95% ordered statistics in the third and sixth columns
reveals that the induced heave effect is less than 1 cm for a short
lever arm.
4. 4 Preliminary water levels
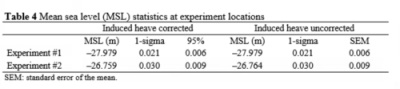
We present the preliminary water level (> 30 days), demonstrating the
concept here. The 1 Hz GNSS solutions were averaged over 3-minute
intervals to mitigate the contributions of surface gravity waves to the
sea surface. Over the simultaneous observation period (Ts> 6 hrs), the
mean sea level to the ellipsoid from the PPP solutions was added to the
mean sea level from the pressure record to reference the pressure record
to the ellipsoid. For this paper, the important uncertainty to quantify
is the mean sea level from the PPP solutions. During Ts, there was a
decrease in the tidal level for experiment 1 and an increase in the
tidal level for experiment 2. This was removed using a quadratic fit to
characterize the uncertainty in water level. The detrended water level
series had a standard deviation of 0.021 and 0.030 m for experiments 1
and 2, respectively. The autocorrelation function for the demean and
detrended time series had a first zero crossing of 21 and 13 lags for
experiments 1 and 2, respectively. Taking only every 21 and 13
observations as statistically independent, for experiments 1 and 2, the
standard error of the mean was 0.006 and 0.009 m, respectively. Refer to
Table 4 for the statistics summary.
Water level anomalies with respect to the NAD83 datum were estimated
through the combinations of the filtered GNSS solutions and using the
combined pressure and hydrographic data obtained at the pressure sensor
location. The water level anomalies at the observation station were
first compared to the corresponding water level anomalies from Dauphin
Island’s NOAA water level station. This was done to determine if
reasonable water levels were estimated at the bottom pattern location.
An estimation of a root mean square difference (rmsd) of 10 cm was
obtained between the two anomalies. A conversion of the water level
anomaly from the GNSS to a pressure anomaly resulted in a more accurate
estimation, with an rmsd of 0.02 dbar (approximately 2 cm) compared to
the pressure anomaly measured during the GNSS observation period. Figure
9 shows that the water level peaks and troughs are aligned. Both water
level anomalies captured three neap tides and two spring tides events.
They also revealed the northern Gulf of Mexico sea level response to a
tropical storm during a neap tide. Based on the correlation between the
two water level anomalies, the ellipsoidally referenced water level from
the pressure sensor will be used in the final tidal datums computations
at the pressure sensor location.

Figure 9 Top panel: water levels referenced to NAD83 datum. Bottom
panel: water level anomalies from the bottom package and a nearby
station.
5. DISCUSSION
Given that the results from the affordable and survey-grade hardware are
very close (1-sigma = 5 cm), it is essential to emphasize that such
positioning performance should not be misconstrued as rendering GNSS+INS
sensors irrelevant in navigation applications. One may be tempted to
reach that conclusion if one considers a unit vector whose origin is at
the sensors, as we have shown here. Contrariwise, that would be far from
true for much longer vectors where the effect of roll and pitch becomes
apparent. A practical example is the case of single-beam and multi-beam
SONARs for seafloor bathymetry relying solely on ray-tracing for
sounding footprint localization on the seafloor, where the effects of
roll and pitch can wrongly place a target some meters away from its
correct locations, depending on the seafloor depth. Nevertheless, one
can safely rely on GNSS-only PPP for positioning applications with very
short antenna lever arms or vectors using a multi-frequency enabled
affordable GNSS receiver in achieving vertical positioning accuracies
better than 10 cm (95% ordered statistics) at an offshore location.
6. CONCLUSION
We describe a new water level measurement technique for tidal datum
extension at offshore locations in addressing vandalization challenges
with GNSS buoys. The technique utilized short-term PPP results from an
affordable GNSS receiver aboard a USV and a pressure sensor deployed on
the seafloor. As a first step toward the proof of concept, we evaluate
the PPP results and show that 5-cm (1 sigma) uncertainty is possible
with an affordable GNSS receiver, provided the PPP processing follows
best practices and the GNSS-derived water levels apply a low-pass
filter. Additionally, we show that a tilt sensor is unnecessary,
provided the antenna lever arm is less than 0.5 m, confirming a
submission from previous work. Accurate lever arm determination using
precise instruments is also vital to overall accuracy. Finally, we
present the preliminary water levels from the pressure sensor referenced
to the ellipsoid. Future work will describe the computational procedure
and analysis for the tidal datum extension in detail.
REFERENCES
- Aggrey, J., Bisnath, S., Naciri, N., Shinghal, G., & Yang, S.
(2019). Accuracy trend analysis of low-cost GNSS chips: The case of
multi-constellation GNSS PPP. Proceedings of the 32nd International
Technical Meeting of the Satellite Division of the Institute of
Navigation, ION GNSS+ 2019, 3618–3635.
https://doi.org/10.33012/2019.16971
- André, B. G., Míguez, B. M., Ballu, V., Testut, L., &
Wöppelmann, G. (2013). Measuring Sea Level with GPS-Equipped Buoys:
A Multi-Instruments Experiment at Aix Island. Measuring Sea Level
with GPS-Equipped Buoys: A Multi-Instruments Experiment at Aix
Island, 10(10), 27–38.
- Arnell, J. T., Ingebrigtsen, I. F., Walb, S., & Roald, E.
(n.d.). A Comparison of Survey-Grade GNSS Receivers by Means of
Observation and Coordinate Domain Approaches; Traditional Vs
Low-Budget. September 2022, 11–15.
- Banville, S., Lachapelle, G., Ghoddousi-Fard, R., & Gratton, P.
(2019). Automated processing of low-cost GNSS receiver data.
Proceedings of the 32nd International Technical Meeting of the
Satellite Division of the Institute of Navigation, ION GNSS+ 2019,
3636–3652. https://doi.org/10.33012/2019.16972
- Bisnath, S., Wells, D., Howden, S., & Stone, G. (2003). The use
of a GPS-equipped buoy for water level determination. Oceans 2003:
Celebrating the Past... Teaming Toward the Future, 3(May 2014),
1241–1246. https://doi.org/10.1109/OCEANS.2003.178031
- Cheng, K., Science, G., & Science, G. (2004). GPS Buoy Campaigns
for Vertical Datum Improvement and Radar Altimeter Calibration.
Program, 470.
- Dodd, D. (2009). Chart Datum Transfer Using a GPS Tide Gauge
Buoy in Chesapeake Bay. International Hydrographic Review, 2.
- Gill, M., Bisnath, S., Aggrey, J., & Seepersad, G. (2018).
Precise Point Positioning (PPP) using Low-Cost and Ultra-Low-Cost
GNSS Receivers. Proceedings of the 30th International Technical
Meeting of The Satellite Division of the Institute of Navigation
(ION GNSS+ 2017), May, 226–236. https://doi.org/10.33012/2017.15123
- Gill, S. K., & Schultz, J. R. (2001). Tidal datums and their
applications, NOAA Special Publication NOS-COPS 1. Retrieved on
1/15/2023 at
https://www.tidesandcurrents.noaa.gov/publications/tidal_datums_and_their_applications.pdf.
- Hare, R., Godin, A., & Mayer, L. (1995). Accuracy Estimation of
Canadian Swath and Sweep Sounding Systems.
- Hocker, B., & Wardwell, N. (2010). Tidal datum determination and
VDatum evaluation with a GNSS buoy. 23rd International Technical
Meeting of the Satellite Division of the Institute of Navigation
2010, ION GNSS 2010, 3, 2076–2086.
- International Hydrographic Organization (IHO; 2020).
International Hydrographic Organization Standards for Hydrographic
Surveys, S-44 Edition 6.1.0. Retrieved on January 16, 2023, from
https://iho.int/uploads/user/pubs/standards/s-44/S-44_Edition_6.1.0.pdf
- Knight, P. J., Bird, C. O., Sinclair, A., & Plater, A. J.
(2020). A low-cost GNSS buoy platform for measuring coastal sea
levels. Ocean Engineering, 203(February), 107198.
https://doi.org/10.1016/j.oceaneng.2020.107198
- Lin, Y. P., Huang, C. J., Chen, S. H., Doong, D. J., & Kao, C.
C. (2017). Development of a GNSS buoy for monitoring water surface
elevations in estuaries and coastal areas. Sensors (Switzerland),
17(1). https://doi.org/10.3390/s17010172
- Lipatnikov, L. A., & Shevchuk, S. O. (2019). Cost-effective
precise positioning with GNSS (Issue 74).
https://www.fig.net/resources/publications/figpub/pub74/figpub74.asp
- Nie, Z., Liu, F., & Gao, Y. (2020). Real-time precise point
positioning with a low-cost dual-frequency GNSS device. GPS
Solutions, 24(1). https://doi.org/10.1007/s10291-019-0922-3
- Nwankwo, U. C., Howden, S., & Wells, D. (2019). Further
Investigations of VDatum to NAD83 Vertical Separations Using United
States Geological Service (USGS) Coastal Water Levels Gage and
Hydrolevel Buoy. U.S. Hydrographic Conference, May 1–12.
- Nwankwo, Uchenna C., Howden, S., Wells, D., & Connon, B. (2020).
Validation of VDatum in Southeastern Louisiana and Western Coastal
Mississippi. https://doi.org/10.1080/01490419.2020.1846644, 44(1),
1–25. https://doi.org/10.1080/01490419.2020.1846644
- Oguntuase, J. O. (2020). Cost-Effective GNSS Hardware for
High-Accuracy Surveys and Its Prospects for Post-Processed Kinematic
( PPK ) and Precise Point Positioning (PPP) Strategies.
Https://Aquila.Usm.Edu/Dissertations/1846.
- Parker, B., Milbert, D., Hess, K., & Gill, S. (2003). National
VDatum - The Implementation of a National Vertical Datum
Transformation Database. Proceedings of the U.S. Hydrographic
Conference, 44(9), 10–15.
- Swanson, R. L. (1974). Variability of tidal datums and accuracy in
determining datums from short series of observations (No. 64).
National Ocean Survey.
- Weston, D. N. D. and, & Dr. Volker Schwieger. (2010). Cost Effective
GNSS Positioning Techniques Cost Effective GNSS Positioning
Techniques (Issue 49).
BIOGRAPHICAL NOTES
Johnson Oguntuase is an Assistant Professor of Hydrographic Science
at the University of Southern Mississippi (USM), where he brings his
expertise to life in the classroom with his teachings in Kinematic
Positioning, Applied Acoustics, and Applied Bathymetry. With a Ph.D. in
Marine Science (Hydrographic Science) and an MSc. in Geodesy, his recent
endeavors show his passion for the field. He is dedicated to developing
cost-effective processing strategies for high-accuracy positioning at
sea using affordable GNSS receivers and tactical-grade INS. Before his
academic career at USM, Dr. Oguntuase was a licensed surveyor and a
successful business owner in Nigeria, where he offered services to
engineering consulting companies and government agencies. He is a member
of the Hydrographic Society of America (THSOA) and a professional member
of the Institute of Navigation (ION).
CONTACTS
Johnson Oguntuase
University of Southern Mississippi
1020 Balch Blvd
Stennis Space Center, MS
USA
Uchenna Nwankwo
Texas A&M Geochemical and Environmental Research Group (GERG)
833 Graham Road,
College Station TX 77845
USA
Stephan Howden
University of Southern Mississippi
1020 Balch Blvd
Stennis Space Center, MS
USA